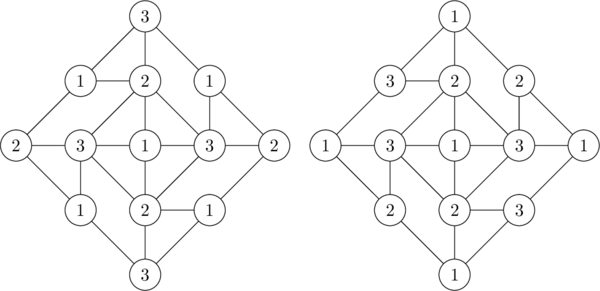
On s’intéresse à une famille de graphes dont les graphes d’intervalles font partis. Il s’agit des graphes cordaux. Tout comme les graphes d’intervalles, on présente un algorithme de coloration pour cette famille.
Exercice
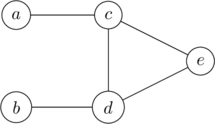
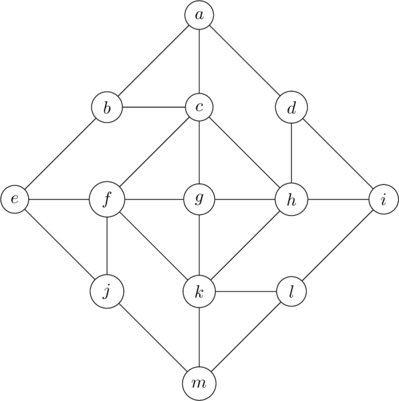
Un graphe est dit cordal si pour tout cycle de taille supérieur ou égale à 4, il existe une corde. C’est à dire qu’il existe une arête entre deux sommets non consécutifs du cycle.
Soit un graphe $G = (S,A)$ connexe. Soit $u$ et $v$ deux sommets de $G$. On appelle séparateur minimale de $u,v$ tout sous-ensemble $V$ de $S$ tel que $u$ et $v$ ne soient pas accessibles dans le graphe induit par les sommets $S \smallsetminus V$ et tel qu’il n’existe pas de sous-ensemble strictement inclus dans $V$ qui vérifie la même propriété.
$1.$ Montrer que les sous-graphes induits d’un graphe cordal sont également des graphes cordaux.
$2.$ Montrer que si tous les séparateurs minimaux de $G$ sont des cliques alors $G$ est cordal.
$3.$ Prouver la réciproque.
Un sommet est dit simpliciale si l’ensemble de ses voisins forment une clique.
$4.$ Montrer par récurrence que tout graphe cordal à plus de deux sommets contient au moins deux sommets simpliciaux. De plus, si le graphe n’est pas complet, il possède deux sommets simpliciaux non adjacents.
On appelle ordre d’élimination parfait de $G$, un ordre sur les sommets $s_1 \lt s_2 \lt \ldots \lt s_n$ de $G$ tels que $s_i$ soit simplicial dans le sous-graphe induit de $G$ par les sommets $s_1, \ldots, s_i$.
$5.$ Montrer qu’un graphe est cordal si et seulement si il admet un ordre d’élimination parfait.
$6.$ En déduire un algorithme de coloration des graphes cordaux et prouver son optimalité.
$7.$ Conclure que les graphes cordaux sont des graphes parfaits.
Correction
$1.$ On note que tout cycle de longueur supérieur ou égale à $4$ dans un sous-graphe induit d’un graphe $G$ est également présent dans $G$. De ce fait, il admet une corde dans $G$ et donc par définition d’un sous-graphe induit, admet une corde dans le sous-graphe induit. Ainsi, tous sous-graphe induit d’un graphe cordal est un graphe cordal.
$2.$ Soit $G$ un graphe dont tous les séparateurs minimaux sont des cliques. S’ils ne possède pas de cycle de longueur supérieur ou égale à $4$, alors il est cordal. Sinon, soit $k\geq4$ et $s_1, s_2, \ldots, s_k$ un cycle de $G$. On s’intéresse à un séparateur minimal de $s_1$ et $s_3$ noté $W$. Comme $(s_1, s_2)$ et $(s_2,s_3)$ sont des arêtes de $G$ on a $s_2 \in W$. De plus, on a $i$ avec $4 \leq i \leq k$ tel que $s_i \in W$ par définition de cycle. Or par hypothèse, $W$ est une clique. Donc, $(s_2,s_i)$ est une arête de $G$.
Ainsi, tout cycle de $G$ de taille supérieur ou égale à $4$ admet une corde. Donc $G$ est cordal.
$3.$ Si $G$ est cordal. On suppose qu’il existe $W$ un séparateur minimal de $G$ qui ne soit pas une clique et qui sépare les sommets $x$ et $y$. Soit $S_1$ et $S_2$ deux composantes connexes du sous-graphes induits par $S \smallsetminus W$. On suppose que $x \in S_1$ et $y \in S_2$. Soit deux sommets $s_1$ et $s_2$ de $W$ qui ne sont pas adjacent.
On rappel que $W$ est un séparateur minimal. De ce fait, $s_1$ et $s_2$ ont tous deux une arête vers $S_1$ et une vers $S_2$. En effet, si tel n’étais pas le cas, par exemple, si $s_1$ n’avait pas d’arêtes vers $S_1,$ alors $W \smallsetminus {s_1}$ serait un séparateur plus petit de $x,y$ ce qui contredit l’hypothèse de minimalité.
On a donc un plus court chemin de $s_1$ vers $s_2$ dans $S_1$ et un plus court chemin de $s_1$ vers $s_2$ dans $S_2$. On a donc un cycle de longueur au moins $4$. Or, ce cycle ne possède pas de cordes. En effet, il n’y a pas d’arêtes entres $S_1$ et $S_2$, $s_1$ et $s_2$ sont non adjacents et s’il existait une corde à l’intérieur de $S_1$ ou $S_2$ on aurait un chemin plus court. Cela contredit donc l’hypothèse de cordalité de $G$.
De ce fait, on a montré que si $G$ est un graphe cordal, alors ses séparateurs minimaux sont des cliques.
$4.$ On note que tous les sommets d’un graphe complet sont simpliciaux.
Soit $\mathcal{P}(n)$ la proposition : « Un graphe cordal non complet à $k$ sommets, où $2\leq k \leq n$, possède deux sommets simpliciaux non adjacents »
Dans le cas d’un graphe à deux sommets, s’il n’est pas une clique, alors le graphe n’a pas d’arêtes. De ce fait, les deux sommets n’ont pas de voisins et sont bien simpliciaux.
Soit $n \geq 2$. On suppose $\mathcal{P}(n)$ vrai et on cherche à prouver $\mathcal{P}(n+1)$.
Soit $G$ un graphe chordal non complet à plus de $2$ sommets. Si $G$ à moins de $n$ sommets, par $\mathcal{P}(n)$ il possède deux sommets simpliciaux non adjacents. Supposons maintenant que $G$ a $n+1$ sommets. Il nous faut juste prouver que $G$ possède deux sommets simpliciaux non adjacents. Soit $W$ un séparateur minimal de $G$ et $S_1$ et $S_2$ deux composantes connexes du sous-graphe induit par $S \smallsetminus W$. On s’intéresse maintenant au sous-graphe induit par $S_1 \cup W$. Si il est complet, alors on considère $x \in S_1$ qui est donc simplicial dans $G$. Sinon, par $\mathcal{P}(n)$, on a deux sommets simpliciaux non adjacents. Or, on rappelle que $W$ est une clique. De ce fait, il existe $x \in S_1$ simplicial dans le sous-graphe induit par $S_1 \cup W$, et donc par définition de $S_1$, simplicial dans $G$. On trouve de même $y \in S_2$ simplicial dans $G$.
On a donc bien trouvé deux sommets simplicial non adjacent, ce qui prouve $\mathcal{P}(n+1)$ et achève la récurrence.
$5.$ Montrons que si un graphe possède un ordre parfait d’élimination alors il est cordal. Soit $G$ un graphe qui possède un ordre parfait d’élimination. Si $G$ n’a pas de cycle de taille supérieur à $4$ alors il est cordal. Sinon, soit $k \geq 4$ et $s_1, \ldots, s_k, s_1$ un cycle de $G$. Sans pertes de généralités, on peut supposer que $s_1$ est le plus grand dans l’ordre d’élimination. Cela implique donc que $s_k$ et $s_2$ sont adjacents. De ce fait, $G$ possède un corde. Il en résulte que $G$ est cordal.
Prouvons maintenant la réciproque et supposons que $G$ est cordal. On sait que tout graphe cordal possède au moins un sommet simplical. De plus, le sous-graphe induit d’un graphe cordal est un graphe cordal. Il en résulte qu’on peut construire un ordre parfait d’élimination de façon décroissante en sélectionnant un sommet simplicial puis en le supprimant avant de recommencer.
Ainsi on a donc qu’un graphe est cordal si et seulement si il possède un ordre parfait d’élimination.
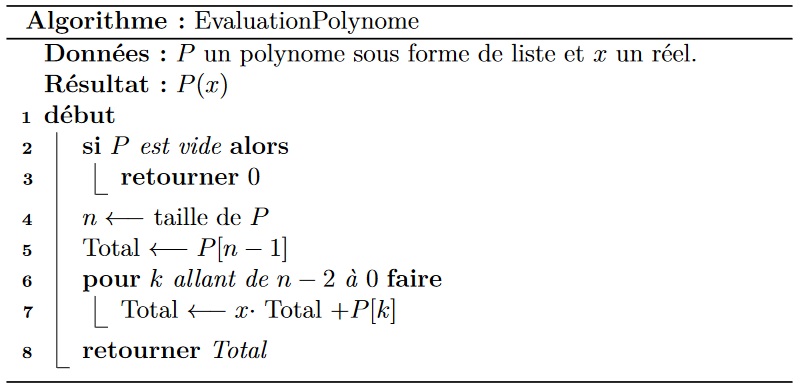
$6.$ On note qu’on a un algorithme qui nous permet de construire l’ordre parfait d’élimination d’un graphe cordal. On visite chaque sommet selon l’ordre d’élimination parfait et on lui assigne première couleur qui n’est pas utilisé pour colorier un de ses voisins déjà visité. Chaque sommet visité fait partie d’une clique de la taille de ses voisins déjà coloré plus un. De ce fait, la couleur attribuée est toujours plus petite ou égale à la taille de la plus grande clique du graphe.
Or la taille de la plus grande clique du graphe est une borne minimal au nombre chromatique. Ainsi, on ne peut utiliser moins de couleurs. Il en résulte que notre coloration est optimale.
$7.$ De la question précédente on en déduit que le nombre chromatique d’un graphe cordal est égale à la taille de sa plus grande clique. De plus, comme le sous-graphe induit d’un graphe cordal est également un graphe cordal, cela reste vrai pour tous ses sous-graphes induits. Il en résulte donc que les graphes cordales sont des graphes parfaits.