Le but de cet exercice est de calculer des puissances et d’évaluer des polynômes en utilisant le moins de multiplications possible. En effet, si on considère généralement que multiplier deux entiers est une opération élémentaire s’effectuant en $O(1)$, cette considération n’est plus possible lorsqu’on considère la multiplication d’entiers très grand, ou encore la multiplication de matrices.
Exercice
On nous donne en entrée $X$ non nul et $p$ des entiers et on cherche à calculer $X^{p}$. On con.sidère que la multiplication de deux entiers se fait en $O(1)$.
$1)$ Donner la complexité du calcul naïf de $X^{p}$.
$2)$ Si $p \gt 2$ est pair, montrer qu’il n’est pas nécessaire de calculer $X^{p-1}$.
$3)$ Donner un algorithme pour calculer $X^{p}$ en utilisant $O\left(\log(p)\right)$ produits et prouver sa correction.
On veut maintenant écrire un algorithme qui prend en entrée un polynôme $\displaystyle P(X) = \sum\limits_{k=0}^{n}X^{k}p_k$ et un réel et qui nous renvoie le polynôme évalué en ce réel.
$4)$ Proposer une façon de représenter les polynômes.
$5)$ Donner un algorithme naïf d’ évaluation. Combien utilise-t-on d’additions et de multiplications ?
$6)$ En mettant $X$ en facteur, donner un algorithme d’évaluation de polynôme.
$7)$ Donner sa complexité en nombre d’additions et de multiplications.
Correction
$1.$ Le calcul naïf de $X^{p}$ correspond à multiplier $p$ fois $X$. On effectue donc $p-1$ produits. Cela correspond alors à une complexité en $O(p)$
$2)$ Posons $p = 2k$. Si on calcul $X^k$, il nous suffit d’effectuer le calcul $X^{k} \times X^{k}$ pour obtenir $X^{2k} = X^{p}$. Il n’est donc pas nécessaire de calculer $X^{p-1}$.
$3)$ On remarque de même que si $p = 2k+1$, on a $X^{p} = X^{k} \times X^{k} \times X$. De là, on propose donc l’algorithme d’exponentiation suivant.

Tout d’abord, on note que $p$ est un entier positif et que l’algorithme s’arrête s’il vaut $0$. De plus, $p$ diminue strictement à chaque nouvel appel de l’algorithme. Ainsi, notre algorithme termine et $p$ est au moins divisé par $2$ à chaque étape. On a donc au plus $O\left(\log(p)\right)$ appels à ExponentiationRapide. De ce fait, ExpoentiationRapide effectue bien $O\left(\log(p)\right)$ produits.
Montrons maintenant par récurrence que notre algorithme est correcte. Soit $\mathcal{P}(n)$ la propriété « ExponentiationRapide($X,p$) calcul $X^{p}$ pour tout entier $X$ non nul et tout entier $p\leq n$. »
On a $\mathcal{P}(0)$ est vrai car pour tout entier $X$ non nul, $X^{0}=1$.
Soit $n \geq 0$. On suppose $\mathcal{P}(n)$. Montrons que $\mathcal{P}(n+1)$ est vraie.
Soit $X$ un entier non nul et $p \leq n+1$. Si $p \leq n$, par hypothèse de récurrence, ExponentiationRapide($X,p$) est bien égale à $X^{p}$. Si $p = n+1$, et que $p$ est impair, on a $k \geq 0$ tel que $p = 2k+1$. Par hypothèse de récurrence, ExponentiationRapide($X,k$) calcul $X^{k}$. De ce fait, ExponentiationRapide($X,p$) calcule bien $X^{p}$. Il en va de même si $p$ est pair.
$4)$ On peut représenter un polynome par une liste de ses coefficients. Ainsi, en indiçant notre liste à partir de $0$, on représente $P$ par une liste $L$ à $n+1$ éléments avec $L[i] = p_i$. L’avantage de ce système est qu’il n’est pas nécessaire de stocker le degré du polynôme.
$5)$ On propose l’algorithme d’évaluation de polynôme suivant.

L’invariant de boucle a considéré pour prouver la correction de notre algorithme est qu’après chaque boucle, Total égale $\displaystyle \sum\limits_{i=0}^{k} x^{i}p_i$.
On utilise donc $n-1$ multiplications pour calculer les puissances de $X$ et $n$ pour calculer les $x^{i}p_i$ avec $i \geq 1$. Ce qui fait alors $2n-1$ multiplications. Pour l’addition, on en effectue une par passage dans la boucle, donc $n$.
$6)$ On remarque la chose suivante :
\begin{align*} P(X) & = p_0 + Xp_{1} + \ldots + X^{n-1}p_{n-1} + X^{n}p_n\\ & = p_0 + X\left(p_{1} + \ldots + X^{n-2}p_{n-1} + X^{n-1}p_n\right)\\ P(X) & = p_0 + X\left(p_1 + X\left(\ldots + X\left(p_n-1 + Xp_n\right)\ldots\right)\right) \end{align*}
Pour $ i \leq n$, on définit les polynômes $P_i$ tel que $\displaystyle P_i(X) = \sum\limits_{k=i}^{n} X^{k-1}p_k$. On a alors, $P(X) = P_0(X)$. Et pour tout $i \lt n $, $P_i(X) = p_i + XP_{i+1}(X)$.
On peut donc proposer l’algorithme de Hörner d’évaluation des polynômes.
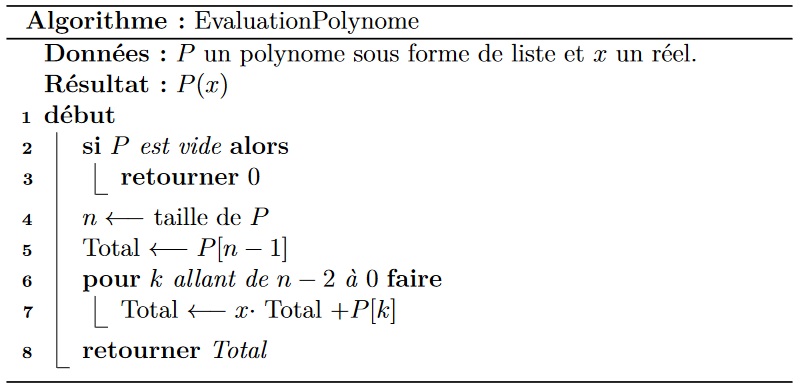
Pour prouver sa correction, on considère l’invariant de boucle suivant : à chaque sortie de boucle, Total a pour valeur $P_k(x)$. Lorsqu’on entre dans la boucle pour la première fois, Total vaut $P_n(x)$. Notre définition des $P_i$ nous assure que l’invariant de boucle reste vérifié après la boucle suivante. Ainsi, à la fin de la dernière boucle, Total vaut $P_0(x) = P(x)$.
$7)$ Notre algorithme utilise cette fois une addition et une multiplication par passage de boucles, soit $n-1$ additions et $n-1$ multiplications.