Exercice
On considère la suite de Fibonnacci définie par :
\[F(0) = 0 \text{ et } F(1) = 1\]
\[\forall n \in \mathbb{N}, F(n+2) = F(n+1) + F(n)\]
Étudions quelques algorithmes de calcul de cette suite.
$1.a)$ Écrire un algorithme récursif prenant en entrée un entier $n$ et retournant $F(n)$.
$b)$ Donner une borne inférieure et une borne supérieure de la complexité de cet algorithme.
$c)$ Écrire un algorithme itératif prenant en entrée un entier $n$ et retournant $F(n)$.
$d)$ Quelle est la complexité en temps de cet algorithme ?
$e)$ Exprimer $F(n)$ en fonction de $n$ et en déduire un algorithme calculant $F(n)$ directement. Calculer sa complexité.
$f)$ Calculer la complexité de l’algorithme récursif.
$2.$ Montrer que pour tout entier $n$, on peut trouver $k$ entiers $c_{i}$ tels que $1 \lt c_{1} \lt c_{2} \lt \cdots \lt c_{k}$ et : \[n = \sum\limits_{i=1}^{k} F(c_{i})\]
$3.a)$ Soit un ensemble fini $Z$ de $\mathbb{N} \smallsetminus {0,1}$ qui ne contient pas d’entiers consécutifs. Soit $m$ le maximum de $Z$. Prouver l’inégalité suivante : $F(m+1) \gt \sum\limits_{k \in Z} F(k)$
$b)$ Prouver l’unicité de la décomposition de tout entier comme somme de termes de la suite de Fibonnacci sans termes consécutifs. C’est le théorème de Zeckendorf.
$4.$ Montrer que le langage $\mathcal{L}$ sur l’alphabet ${0,1}$ contenant le mot vide et les mots ne possédant pas deux $1$ consécutifs mais terminant par $1$ est régulier.
Soit $u$ un mot de $\mathcal{L}$ de longueur $|u|$. Pour tout $k \leq |u|$, on pose $u(k) = 0$ si la $k$-ième lettre de $u$ est $0$ et $u(k) = 1$ sinon. Soit $n$ un entier. On dit que $u$ est la représentation de Zeckendorf de $n$ si :
\[n = \sum\limits_{k=1}^{|u|} u(k)F(k+1)\]
Cette représentation est unique.
$5.$ Quelle est la longueur de la représentation d’un entier ?
Correction
$1.$ a) On propose l’algorithme suivant:

b) Soit $T(n)$ le nombre d’opérations nécessaires pour calculer $F(n)$ avec cet algorithme récursif. On a une constante $c$ telle que : \[T(0) = T(1) = c\]
\[\forall n \in \mathbb{N}, T(n+2) = T(n+1) + T(n) +c\]
On a $T(n+1) \geq T(n)$ donc pour $n\geq 2$:
\begin{align*} T(n) & \leq 2T(n-1) + c\\ & \leq 4T(n-2) + 2c + c\\ & \leq 2^{n-1}T(1) + 2^{n-2}c + \ldots + 2c + c T(n)\\ & \leq (2^{n}-1)c \end{align*}
Donc $\displaystyle \boxed{T(n) = O\left(2^{n}\right)}$. Pour la borne inférieure, on effectue un calcul similaire :
\begin{align*}
T(n) & \geq 2T(n-2) + c\\
& \geq 4T(n-4) + 2c + c\\
T(n) & \geq (2^{\left\lfloor \frac{n+2}{2}\right\rfloor}-1)c
\end{align*}
On obtient donc $\displaystyle \boxed{T(n) = \Omega\left(2^{\frac{n+2}{2}}\right)}$.
$c)$ On propose cet algorithme.

$d)$ La création du tableau nous coûte $\Theta(n)$ opérations, chaque appel de boucle nous coûte $\Theta(1)$ et nous effectuons $n-2$ appels. Ainsi, la boucle correspond à $\Theta(n)$ opérations. Ainsi, notre algorithme a une complexité en temps en $\Theta(n)$.
e) Pour trouver la valeur de $F(n)$, nous commençons par résoudre l’équation caractéristique associée : $r^{2}-r-1=0$. Elle a pour solutions $\varphi$ et $\varphi’$ où $\displaystyle \varphi = \frac{1+\sqrt{5}}{2}$ et $\displaystyle\varphi’ = \frac{1-\sqrt{5}}{2}$. On a donc $\alpha$ et $\beta$ tels que :
\[\forall n \in \mathbb{N}, F(n) = \alpha\varphi^{n} + \beta\varphi’^{n}\]
Pour trouver la valeur de $\alpha$ et $\beta$, on considère les conditions initiales : $F(0) = 0$ et $F(1) = 1$.
\[\left\{\begin{matrix} \alpha + \beta = 0 \\ \alpha\frac{1+\sqrt{5}}{2} + \beta\frac{1-\sqrt{5}}{2} = 1\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \alpha + \beta = 0 \\ \alpha – \beta = \frac{2}{\sqrt{5}}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \alpha = \frac{1}{\sqrt{5}} \\ \beta = -\frac{1}{\sqrt{5}}\end{matrix}\right. \]
Ainsi $\displaystyle F(n) = \frac{1}{\sqrt{5}}\left(\varphi^{n}-\varphi’^{n}\right)$.
On peut écrire un algorithme renvoyant directement $F(n)$ en utilisant cette formule. Pour cela, on utilise l’exponentiation rapide (voir l’exercice correspondant pour plus d’informations) qui nous donne $\varphi^{n}$ et $\varphi’^{n}$ en $\Theta(\log(n))$ multiplications.Toutefois, il est important de conserver une précision suffisante dans notre calcul.
$f)$ Il existe plusieurs façons de calculer la complexité en temps de notre algorithme récursif. L’idée principale est de montrer que le terme constant est négligeable pour se ramener à l’équation $T(n+2)=T(n+1)+T(n)$ qu’on vient de résoudre. Nous en proposons une schématique.
Nous pouvons tracer l’arbre binaire des appels récursifs successifs à notre fonction. Ainsi, chaque noeud correspond à un appel récursif qui nous coûte $c$, chaque feuille correspond à une exécution de notre fonction sur l’entrée $0$ ou $1$ qui coûte également $c$.
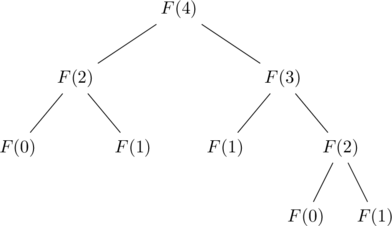
On note que si on appelle récursivement en $0$ alors on appelle également en $1$. C’est pourquoi, le nombre de feuilles étiquetées par $F(1)$ et supérieur au nombre de feuilles étiquetées par $F(0)$. De plus, $F(n)$ est égal à la somme des valeurs des feuilles qui valent au plus $1$. On a donc entre $F(n)$ et $2F(n)$ feuilles. On rappelle que le nombre de n\oe{}uds internes d’un arbre binaire est égal à son nombre de feuilles moins un. Ainsi, en comptant les feuilles, on a entre $F(n)$ et $4F(n)$ noeuds. De ce fait, la complexité de notre algorithme est comprise entre $F(n)c$ et $4F(n)c$. La question précédente nous permet donc de conclure que la complexité temporelle de l’algorithme récursif est en $\displaystyle \boxed{\Theta\left(\varphi^{n}\right)}$.
$2.$ On procède par récurrence forte sur l’ensemble des entiers naturels pour prouver la propriété $\mathcal{H}(n) = $ « Il existe $k$ entiers $c_{i}$ qui nous conviennent ». Pour $n=0$, il nous suffit de considérer la somme vide.
On suppose la propriété vraie jusqu’au rang $n\geq0$, montrons qu’elle le reste au rang $n+1$. On a $n+1 \geq F(2)$. De ce fait, on peut considérer le plus grand $m\geq2$ tels que $n+1 \geq F(m)$.
Par hypothèse, $\mathcal{H}(n+1-F(m))$ est vraie. Soit $k \in \mathbb{N}$ et $1 \lt c_1 \lt \cdots \lt c_k$ tels que $n+1-F(m) = \sum\limits_{i=1}^{k} F(c_{i})$. On note que pour tout $x \geq 2$, $F(x+1) \lt 2F(x)$. Comme $n+1 \lt F(m+1)$, on obtient $n+1-F(m) \lt F(m)$. Cela signifie donc que $c_k$ est strictement inférieur à $m$. On considère donc la suite $c_1 \lt \cdots \lt c_k \lt m$ qui convient pour $n+1$ ce qui prouve $\mathcal{H}(n+1)$ et achève la récurrence.
$3.$ a) On procède par récurrence forte sur $m$, le maximum de notre ensemble $Z$. La propriété« Tout ensemble $Z$ qui satisfait nos conditions et dont le plus grand élément est $m$ vérifie l’inégalité » est vraie au rang $m=2$ et $m=3$ car $2 \gt 1$ et $3 \gt 2$. On suppose la propriété vraie jusqu’au rang $m\geq2$. Montrons qu’elle le reste au rang $m+1$.
Soit $Z$ un ensemble fini de $\mathbb{N} \smallsetminus {0,1}$, tel que son maximum soit $m+1$ et qu’aucun nombre consécutif ne soit dans $Z$. Le deuxième plus grand élément de $Z$ est au plus $m-1$. De ce fait on a par hypothèse de récurrence et par croissance de $F$, $F(m) \gt \sum\limits_{k\in Z \smallsetminus {m+1}} F(k)$. Donc on a :
\[F(m+2) = F(m+1) + F(m) \gt \sum\limits_{k\in Z} F(k)\]
Ce qui prouve la propriété au rang $m+1$ et achève la récurrence.
$b)$ On procède par récurrence forte, similairement à $2$. On ajoute que par le lemme précédent, pour tout entier n, le plus grand $m$ telle que $F(m) \leq n$ est dans notre séquence et que si $F(m-1)$ est inférieur à $n – F(m)$ on aurait $F(m+1)$ inférieur à $n$, contredisant la définition de $m$.
$4.$ Les langages rationnels sont stables par complémentaires et le langage des mots contenant $11$ est rationnel, comme le montre l’expression $(0+1)^{*}11(0+1)^{*}$. Ainsi, le langage des mots ne contenant pas $11$ est rationnel. De plus, les langages rationnels sont stables par intersection, donc par intersection avec $(0+1)^{*}1$ le langage des mots ne contenant pas $11$ et se terminant par $1$ est rationnel. Enfin, les langages rationnels sont stables par union, donc le langages contenant le mot vide et les mots ne contenant pas $11$ mais se terminant par $1$ est rationnel.
$5.$ La longueur de la représentation de $0$ est $0$ car il s’agit du mot vide. Pour un entier strictement positif n, cette longueur correspond à $m-1$ où $m$ est le plus grand entier tel que $F(m) \lt n$. De plus $\varphi’^{n}$ est négligeable devant $\varphi^{n}$. Ainsi, la longeur de la représentation de $n$ est $\left\lfloor \log_{\varphi}\left(n\right) \right\rfloor$.