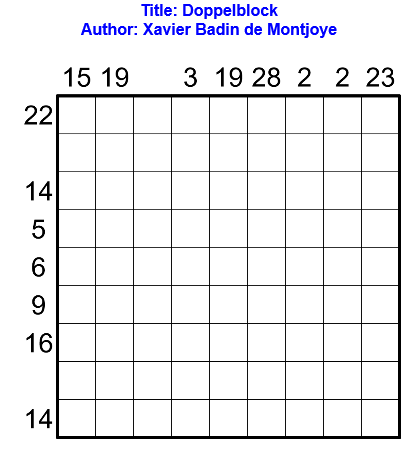
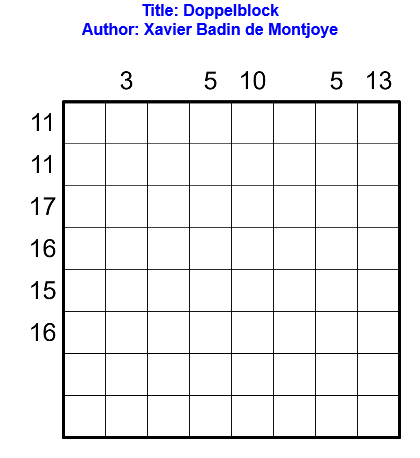
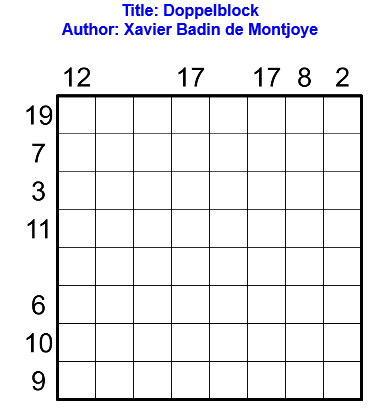
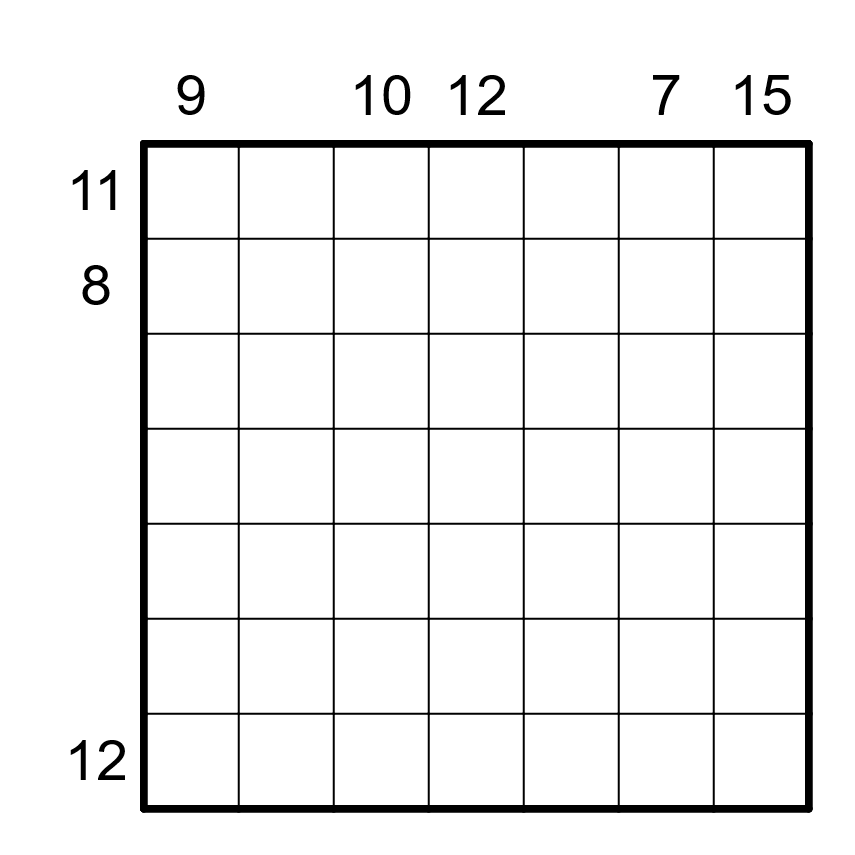
Règles
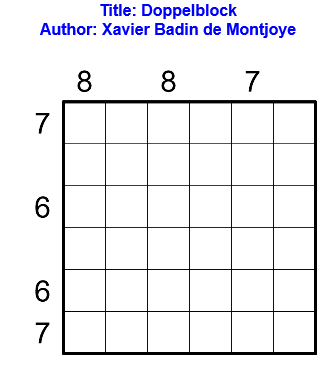
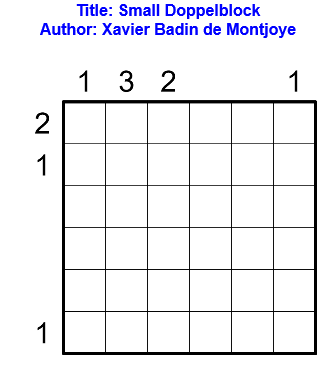
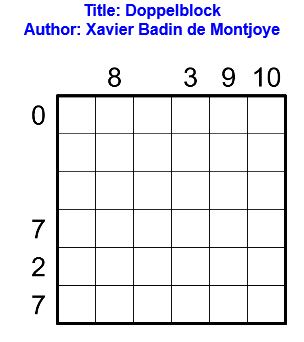
Les règles du doppelblock sont les suivantes : noircir exactement deux cases dans chaque ligne et chaque colonne. Dans les cases restantes, il faut placer un entier entre 1 et X-2, où X est le nombre de cases dans chaque ligne, de telle sorte que chaque nombre apparaisse une et une seule fois dans chaque ligne et chaque colonne. Les nombres à l’extérieur de la grille indiquent la somme des entiers entre les deux cases noircies dans la ligne ou colonne correspondante. Le contenu de certaines cases peut déjà être donné.
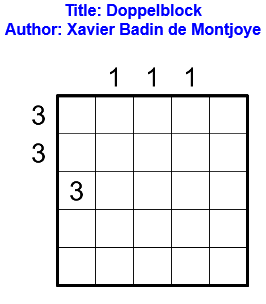
Exemple
Voici un exemple de grille de doppelblock et sa solution.
Résoudre l’exemple en ligne.
Histoire du doppelblock
D’après le WPC unofficial wiki, le doppelblock apparaît dans les qualifications pour la compétition de puzzle Japonaise de 2006 par un auteur inconnu. Il a ensuite été inventé indépendamment en 2008 par Naoki Inaba (Japon)