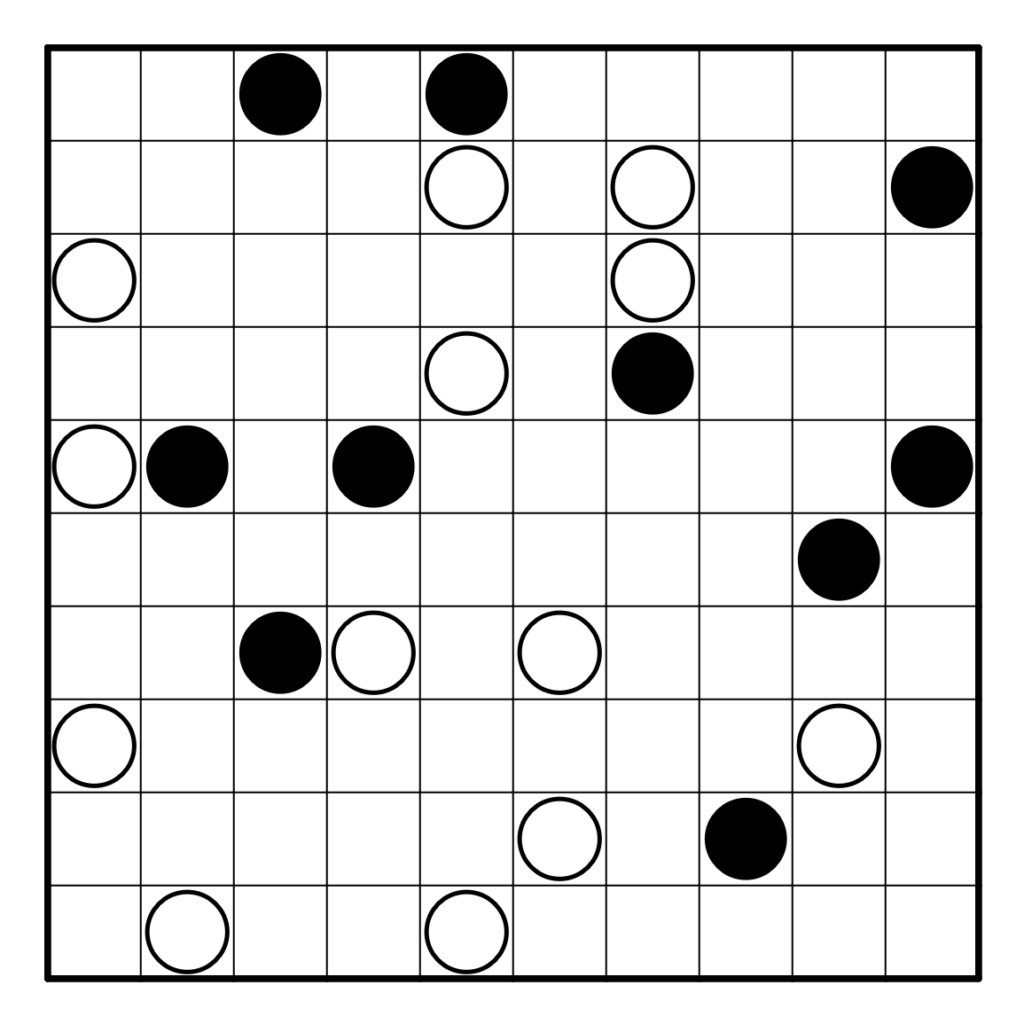
Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu

Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu
Les règles du Masyu sont les suivantes : Tracer une unique boucle passant orthogonalement par le centre de certaines cases ne se croisant pas. La boucle doit tourner dans les cercles noirs et aller tout droit dans les cases précédentes et suivantes. La boucle doit aller tout droit dans les cercles blancs, mais tourner soit juste avant, soit juste après chaque cercle blanc.
Voici un exemple de grille de Masyu et sa solution.
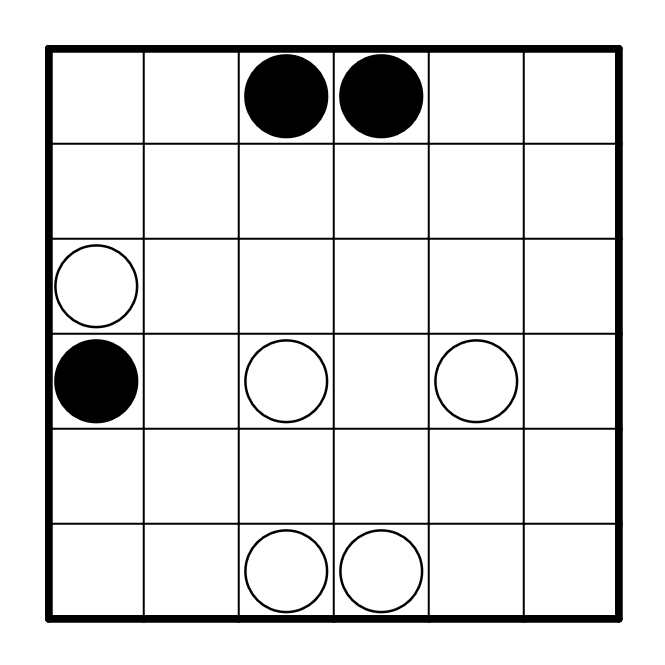
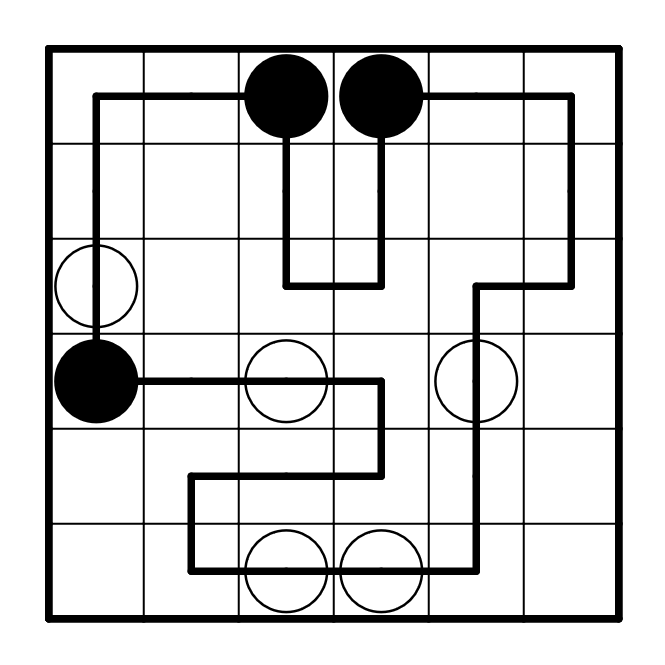
Résoudre l’exemple en ligne.
D’après Wikipedia et le WPC unofficial wiki, Masyu est un puzzle créé et publié par Nikoli d’abord en 1999 avec uniquement des ronds blancs et ensuite à partir de 2000 dans sa version telle qu’on la connait actuellement.
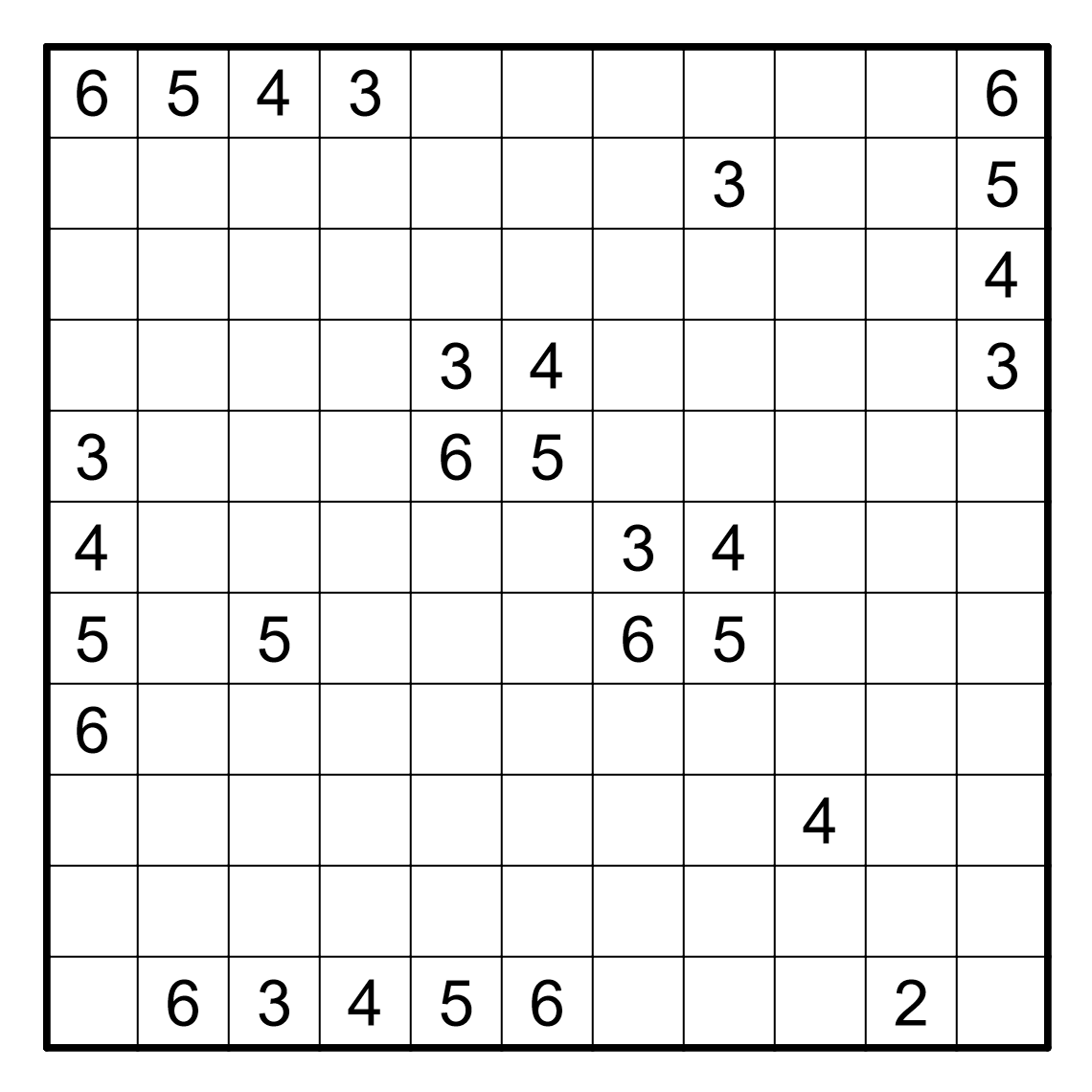
Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.
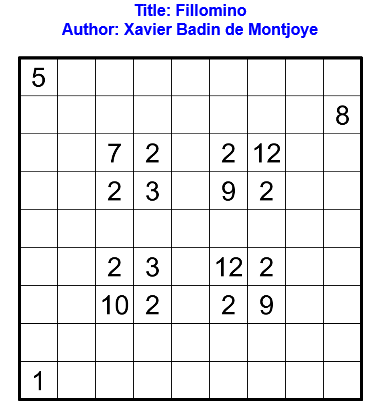
Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.
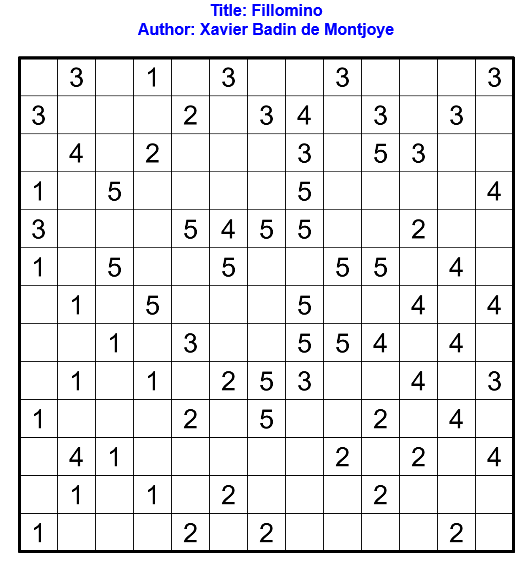
Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.
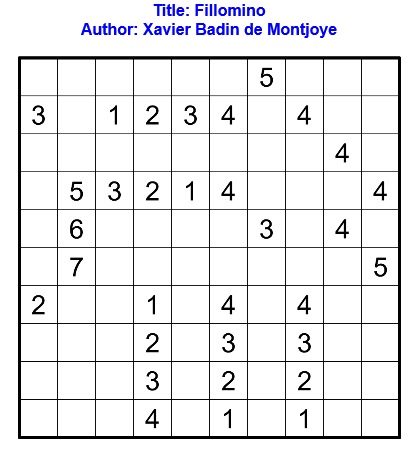
Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.
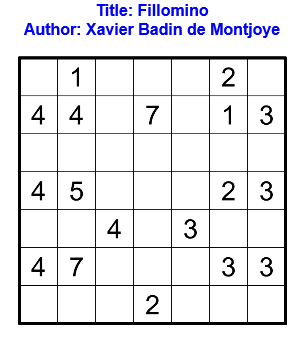
Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.

Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.

Résoudre en ligne ici. Pour la vérification automatique, tracer les bordures des régions.
Règles : Règles du Fillomino Classique.
Les règles du fillomino sont les suivantes : placer un entier par case telles que les conditions suivantes soient réunies :
Certains nombres sont déjà inscrits dans la grille.
On remarque donc que pour résoudre une grille, on peut se contenter de donner les bordures des régions, ou de remplir tous les nombres.
Voici un exemple de grille de fillomino et sa solution.
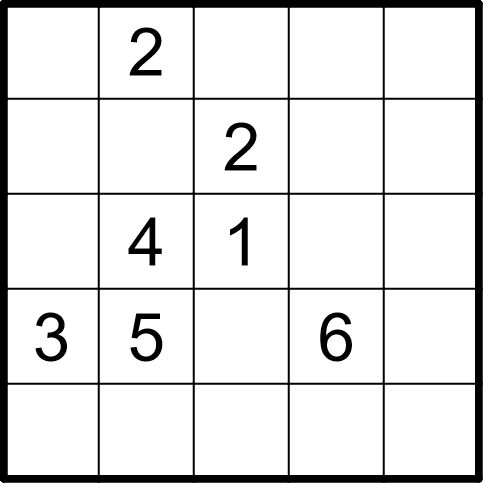
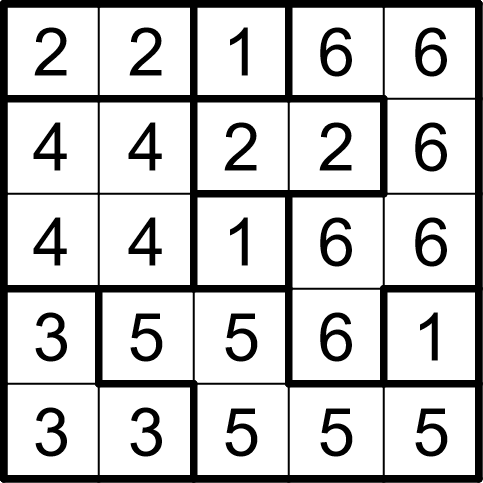
Résoudre l’exemple en ligne.
D’après le WPC unofficial wiki et GMPuzzles, le fillomino est un puzzle apparaissant pour la première fois dans Nikoli en 1994.