
Résoudre en ligne ici !
Règles : Règles classiques du Shakashaka.
Les règles de Shakashaka sont les suivantes : dans certaines cases vides, placer un triangle rectangle occupant exactement la moitié de la cellule, la coupant sur une des grandes diagonales. Tout espace non coloré doit être rectangulaire. Un nombre dans une cellule indique le nombre de cases contenant un triangle orthogonalement adjacentes à la cellule. Ainsi, il y a cinq possibilités pour chaque case vide : la laisser vide, ou placer un des quatre triangles rectangles suivants : ◢, ◣, ◤, ◥.
Voici un exemple de grille de Shakashaka et sa solution :


Résoudre l’exemple en ligne ici.
Pour résoudre un puzzle Shakashaka en utilisan Penpa+, il y a deux possibilités : dans l’onglet Composite > Paint > Shakashaka, un clic place un point dans la case, qui n’est pas pris en compte dans la vérification, et un clic en glissant vers un des coins de la cellule place un triangle pointant vers ce coin.
L’autre possibilité est dans l’onglet Shape > Shape > ◢ ◣ ◤ ◥. Si la fenêtre contenant les triangles n’apparait pas, passer Panel en On.
Si ces onglets ne sont pas accessibles, dans le menu déroulant nommé Tab, cliquer sur Disable Penpa Lite.
Shakashaka est un puzzle développé et publié par Nikoli.
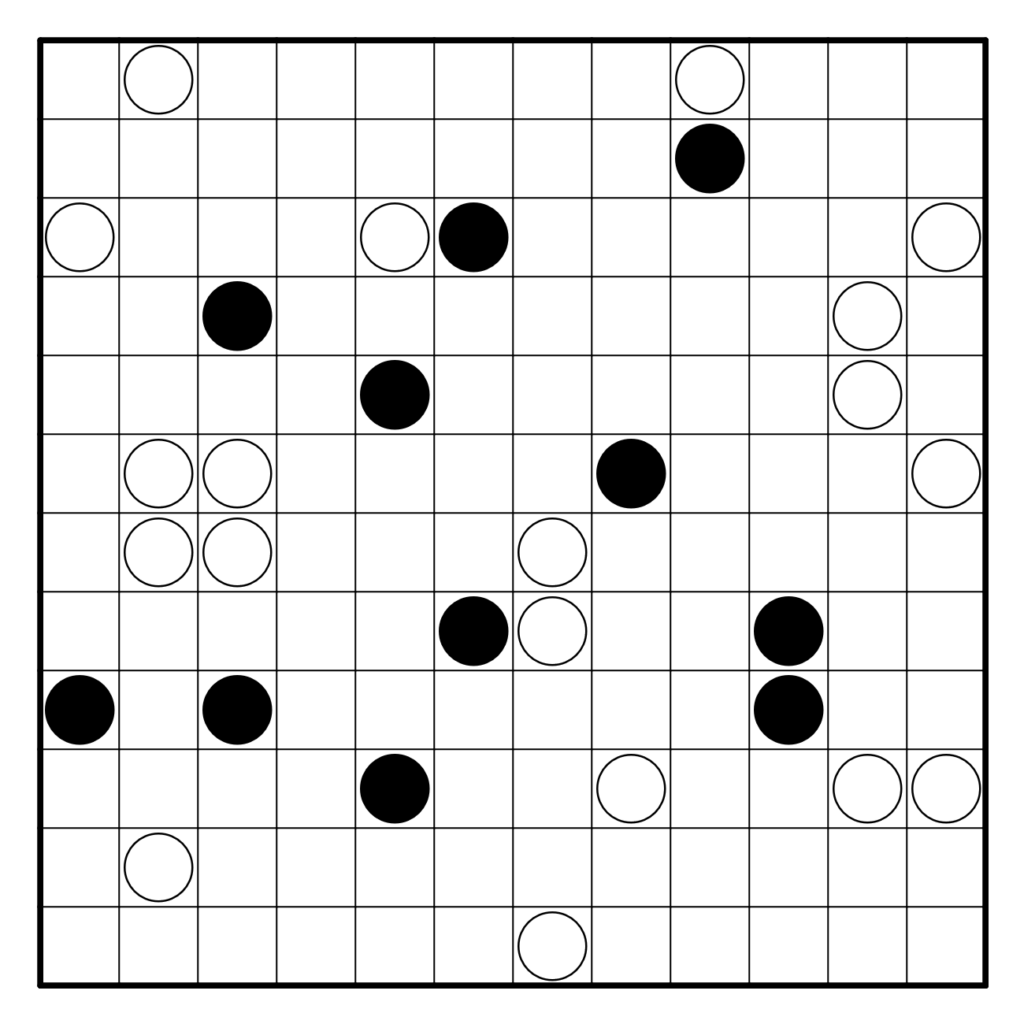
Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu

Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu

Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu

Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu
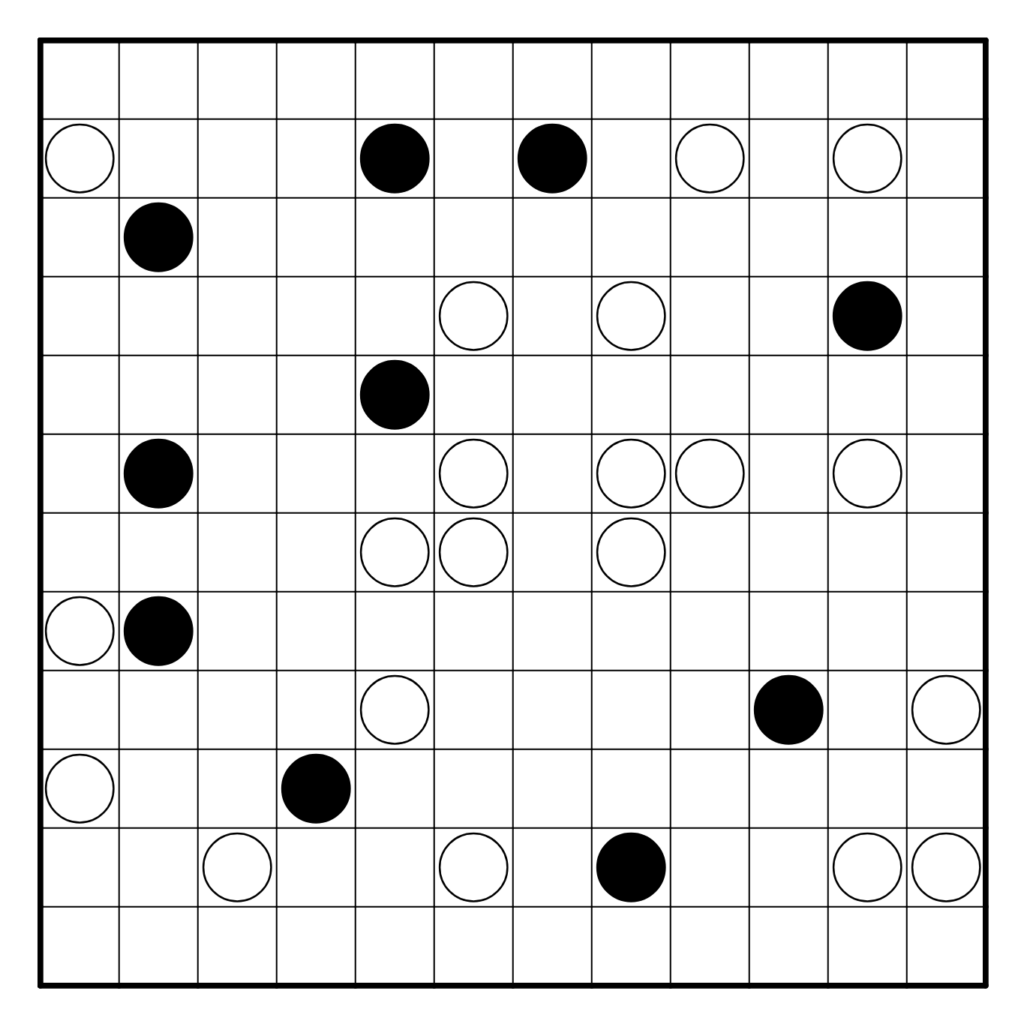
Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu
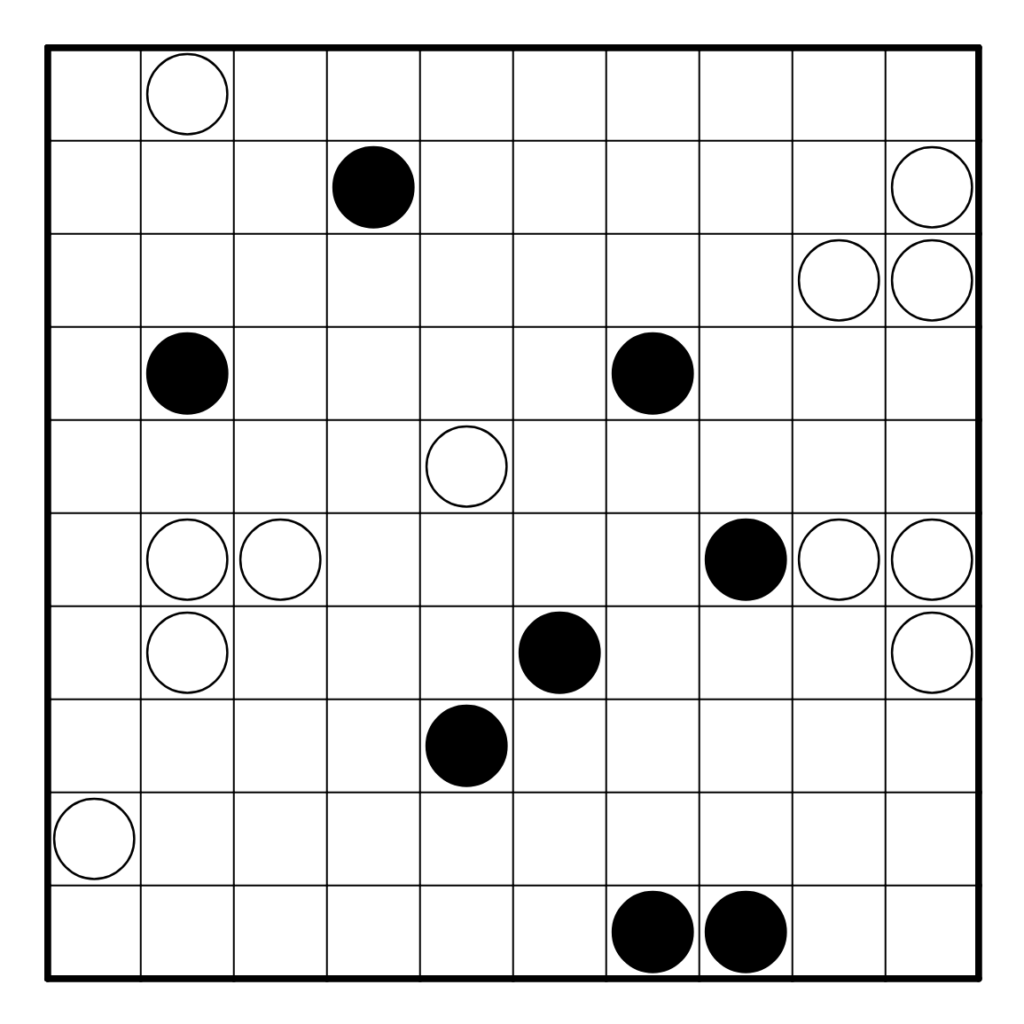
Résoudre en ligne ici ! Pour la vérification automatique, tracer correctement la boucle.
Règles : Les règles classiques du Masyu