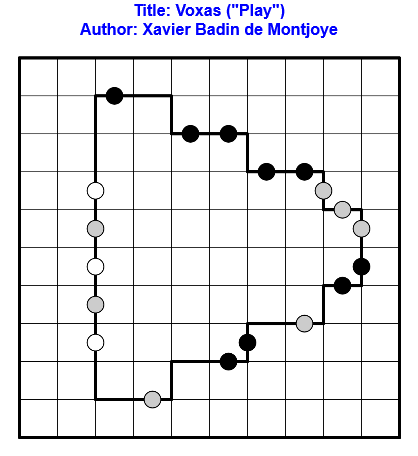
Résoudre en ligne ici !
Règles : Règles classiques de Voxas.
Après avoir mis en Pause hier, on appuie sur Play aujourd’hui !

Résoudre en ligne ici !
Règles : Règles classiques de Voxas.
Après avoir mis en Pause hier, on appuie sur Play aujourd’hui !
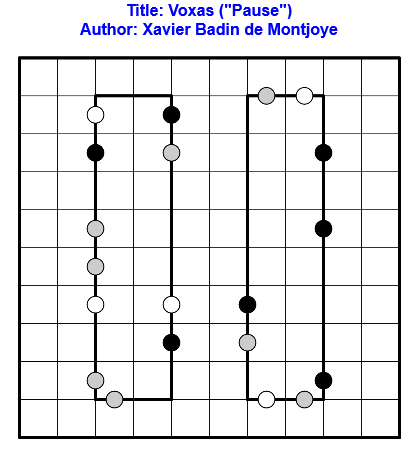
Résoudre en ligne ici !
Règles : Règles classiques de Voxas.
On appuie sur Pause aujourd’hui et Play demain !

Résoudre en ligne ici !
Règles : Règles classiques de Voxas.
Un Voxas vide sans tous ses points pour commencer la semaine.
Les règles de Voxas sont les suivantes : Diviser la grille en rectangle de taille 1×2 ou 1×3 d’orientation horizontale ou verticale. Les bords de certains rectangles sont déjà donnés. Une arête avec un rond blanc sépare deux rectangles de même taille et même orientation. Une arête avec un rond noir sépare deux rectangles de taille et orientation différentes. Une arête avec un rectangle sépare deux rectangles ayant soit la même taille, soit la même orientation, mais pas les deux.
Voici une grille de Voxas et sa solution
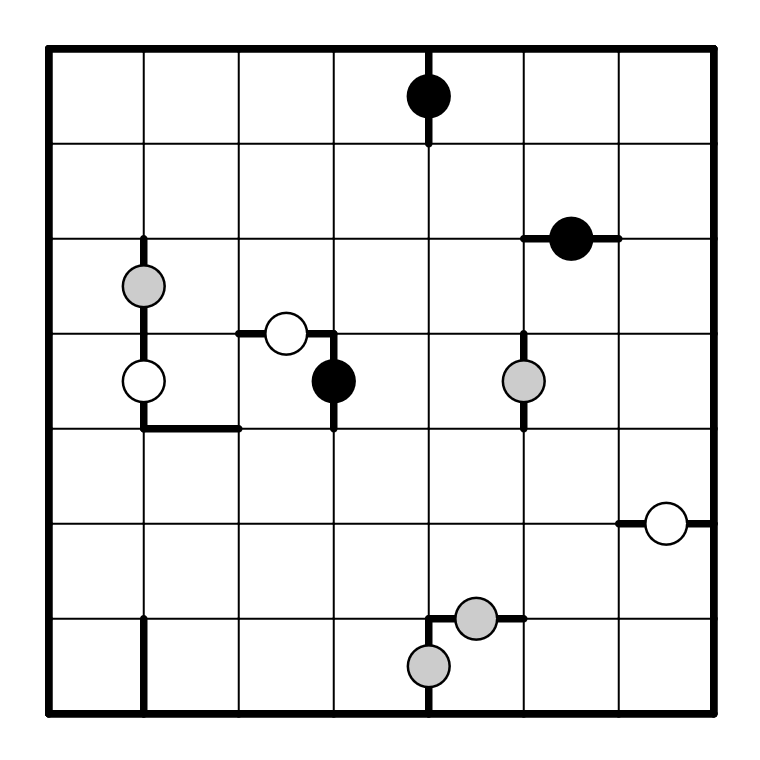
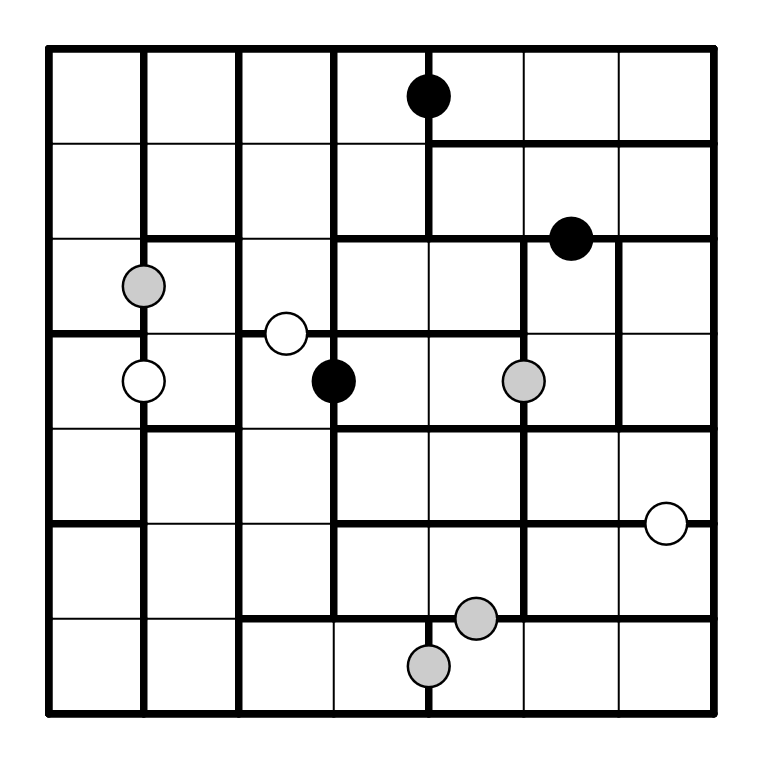
Résoudre en ligne ici.
Voxas est un Puzzle créé par Eric Fox.